今天主要来聊聊分子的振动模式。首先，我们来介绍一下分子的振动自由度。分子的运动由平动、转动和振动三部分组成。假设一个分子中的原子数为N，则该分子总共具有3N个运动自由度，其中需要3个空间坐标来确定分子质心的位置，3个坐标来确定分子在空间的取向（如果是直线分子，则只需要2个坐标即可），由此我们可以得出对于非直线分子，振动自由度为3N-6；而对于直线分子，振动自由度为3N-5。让我们以氧气分子为例，由于是双原子分子，故只有一个振动自由度。显然该振动是中心对称的。非对称振动对应红外吸收，而对称振动对应拉曼散射。对于氧气分子，由于没有任何偶极矩的变化，自然可以对应上面的结论，作为一个中心对称的分子，是没有红外吸收光谱的。让我们再来看另外一个例子，一氧化氮（NO），由于既有极性变化，也有偶极矩变化，因此它同时具有拉曼光谱以及红外光谱。

以上说到的都是双原子分子，现在，我们来看一些三原子分子。根据对振动自由度的计算方式，三原子分子具有3个振动模式：对称伸缩振动、弯曲/变形振动、不对称伸缩振动。具体表现形式如下所示：

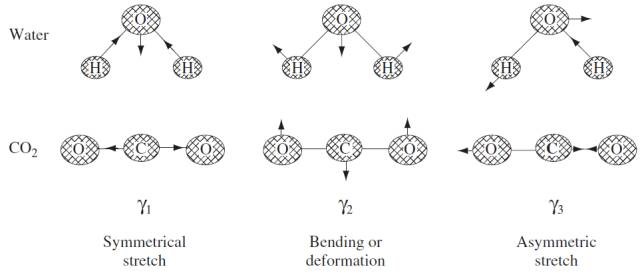
上图展示了H2O和CO2分子的三种振动模式，采用了小球弹簧模型，不知道大家还是否记得中学时候学过的胡克定律，小球即原子，弹簧即化学键。弹簧越紧，小球质量越轻，振动频率就越高。

该模型被广泛用于解释振动光谱，然而，对于分子而言，除了化学键和原子以外，电子浓度也是一个变量。随着分子的振动，电子云的变化会引起分子偶极矩或者极性的变化。对于三原子分子而言，对称伸缩振动将引起极性变化从而带来强拉曼散射，而变形振动则会引起偶极矩变化，从而导致强红外吸收。

以上分析均只针对于小分子，对于复杂的大分子而言，对其振动的分析将更加困难。我们需要将每个小分子的振动光谱都计算出来，而由于大分子本身的复杂性，目前要完成这样的计算几乎不可能。现在的做法是将一个振动分子的混乱内部结构看作是由许多相当简单的振动组合而成的，应用群论来对分子的振动模式进行分析。

文章来源：拉曼光谱公众号
文章链接：分子的振动模式
文字报道：袁伟
文章编辑：董荣录